Question

NCERT Solutions Class 12 Maths Chapter 5 Continuity and Differentiability is suitable for studying for CBSE board exams and it is made by the experts in the subject matter. NCERT Solutions is one of the best study materials for students of class 12.

NCERT Solutions Class 12 is designed according to the latest syllabus proposed by the experts to provide complete detail of NCERT intext questions and also back of the chapter questions.

• Continuity – the concept of rigorous formulation and the intuitive concept of any function which have no breaks or jumps is termed continuity. Continuity can also be defined as the \(x\)-values when it is closer to the -values of the function. The concept of continuity can also be defined according to the saying of the function \(f(x)\) is continuous at any given point.
• Differentiability – a derivative that exists at each point in the domain of a function that has derivatives. A differential function when plotted in a graph has a non-vertical tangent line at the interior of the domain.
• Algebra of continuous functions – there are four basic arithmetic operations for carrying out operations on continuous algebraic functions. These four arithmetic functions are
  1. Addition operation of the continuous functions
  2. Subtraction of continuous functions
  3. Multiplication of continuous functions
  4. Division of continuous functions
• Derivatives of composite functions – we can define the derivative of composite functions as the product of the derivative of the inside function concerning the outside function. The composite functions of the derivatives are formed with the help of the chain rule formula.
• Derivatives of implicit functions – a dependent and the independent variable which is written in the form of \(y-3x^2+2\)
• Derivatives of inverse trigonometric functions \(-x+5 =0\) then the function is called an implicit function.

functions	\(( {dy \over dx})\)
arcsin x	\({1 \over \sqrt{1-x^2}}\)
arccos x	\(- {1 \over \sqrt{1-x^2}}\)
arctan x	\({1\over {1+x^2}}\)
account x	\(-{1\over {1+x^2}}\)
arcsec x	\({1 \over |x|\sqrt{x^2-1}}\)
arccsc x	\(-{1 \over |x|\sqrt{x^2-1}}\)

• Logarithmic Differentiation – the logarithmic differentiation is the method to calculate differentiated functions with the help of employing the logarithmic derivative of a given function \(f\).

NCERT Solutions Class 12 Maths is prepared by the mentors who have years of experience in the subject matter.

Answer 1

84. If x and y are connected parametrically by the equation, without eliminating the parameter, find \(\frac{dy}{dx}\).

\(x = a\left(cos \,t + log\,tan\frac12\right), y = a\,sin\,t\) 

Answer:

The given equations are \(x = a\left(cos \,t + log\,tan\frac12\right), y = a\,sin\,t\) 

85. If x and y are connected parametrically by the equation, without eliminating the parameter, find \(\frac{dy}{dx}\).

x = a secθ, y = b tanθ

Answer:

The given equations are x = a secθ, y = b tanθ

 

86. If x and y are connected parametrically by the equation, without eliminating the parameter, find \(\frac{dy}{dx}\).

x = a(cosθ + θsinθ), y = a(sinθ - θcosθ)

Answer:

The given equations are x = a(cosθ + θsinθ), y = a(sinθ - θcosθ)

87. Find the second order derivatives of the function.

x² + 3x + 2

Answer:

Let y = x² + 3x + 2

Then,

88. Find the second order derivatives of the function.

x²⁰

Answer:

Let y = x²⁰

Then,

89. Find the second order derivatives of the function.

x.cosx

Answer:

Let y = x.cosx

Then,

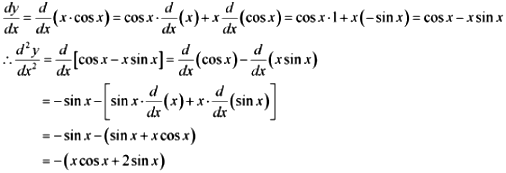
90. Find the second order derivatives of the function.

log x

Answer:

Let y = log x

Then,

91. Find the second order derivatives of the function.

x³ log x

Answer:

Let y = x³ log x

Then,

92. Find the second order derivatives of the function.

e^x sin5x

Answer:

Let y = e^x sin5x

Then,

93. Find the second order derivatives of the function.

e^6x cos3x

Answer:

Let y = e^6x cos3x

Then,

94. Find the second order derivatives of the function.

tan^-1 x

Answer:

Let y = tan^-1 x

Then,

95. Find the second order derivatives of the function.

log(log x)

Answer:

Let y = log(log x)

Then,

96. Find the second order derivatives of the function.

sin(log x)

Answer:

Let y = sin(log x)

Then,

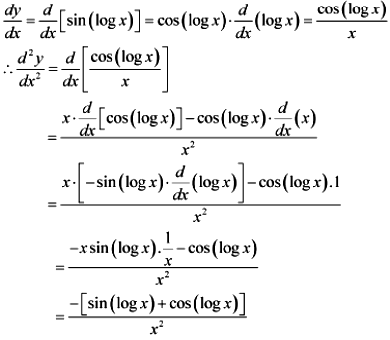
97. If y = 5cos x - 3sin x, prove that \(\frac{d^2y}{dx^2} + y = 0\)

Answer:

It is given that, y = 5cos x - 3sin x

Then,

Hence, proved.

98. If y = cos^-1 x, find \(\frac{d^2y}{dx^2} \) in terms of y alone.

Answer:

It is given that, y = cos^-1 x

Then,

99. If y = 3 cos(log x) + 4sin(log x), show that x²y₂ + xy₁ + y = 0

Answer:

It is given that, y = 3 cos(log x) + 4sin(log x)

Then,

100. If y = 500e^7x + 600e^-7x, show that \(\frac{d^2y}{dx^2} = 49y\) 

Answer:

It is given that, y = 500e^7x + 600e^-7x

Then,

Hence, proved.

101. If e^y(x + 1) = 1, show that \(\frac{d^2y}{dx^2} = \left(\frac{dy}{dx}\right)^2\) 

Answer:

The given relationship is e^y(x + 1) = 1

Taking logarithm on both the sides, we obtain 

Differentiating this relationship with respect to x, we obtain

Hence, proved.

102. If y = (tan^-1 x)², show that (x² + 1)² y₂ + 2x(x² + 1) y₁ = 2

Answer:

The given relationship is y = (tan^-1 x)²

Then,

Again differentiating with respect to x on both sides, we obtain 

Hence, proved.

Answer 2

103. Verify Rolle’s Theorem for the function f(x) = x² + 2x - 8, x ∈ [-4, 2]

Answer:

The given function, f(x) = x² + 2x - 8, being a polynomial function, is continuous in [−4, 2] and is differentiable in (−4, 2).

∴ f (−4) = f (2) = 0 

⇒ The value of f (x) at −4 and 2 coincides. 

Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that f'(c) = 0

104. If f : [-5, 5] → R is a differentiable function and if f'(x) does not vanish anywhere, then prove that f(-5) ≠ f(5).

Answer:

It is given that f : [-5, 5] → R is a differentiable function. 

Since every differentiable function is a continuous function, we obtain 

(a) f is continuous on [−5, 5]. 

(b) f is differentiable on (−5, 5). 

Therefore, by the Mean Value Theorem, there exists c ∈ (−5, 5) such that

It is also given that f'(x) does not vanish anywhere.

Hence, proved.

105. Verify Mean Value Theorem, if f(x) = x² - 4x - 3 in the interval [a, b], where a = 1 and b = 4

Answer:

The given function is f(x) = x² - 4x - 3

f, being a polynomial function, is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4.

Mean Value Theorem states that there is a point c ∈ (1, 4) such that f'(c) = 1

Hence, Mean Value Theorem is verified for the given function.

106. Verify Mean Value Theorem, if f(x) = x³ - 5x² - 3x in the interval [a, b], where a = 1 and b = 3. Find all c ∈ (1, 3) for which f'(c) = 0

Answer:

The given function f is f(x) = x³ - 5x² - 3x

f, being a polynomial function, is continuous in [1, 3] and is differentiable in (1, 3) whose derivative is 3x² − 10x − 3.

Mean Value Theorem states that there exist a point c ∈ (1, 3) such that f'(c) = -10

Hence, Mean Value Theorem is verified for the given function and c = \(\frac73\)∈ (1, 3) is the only point for which f'(c) = 0