Question

NCERT Solutions Class 12 Maths Chapter 8 Applications of Integrals is prepared by the mentors who have the expertise in the subject. Our NCERT Solutions is best suitable for students of class 12. NCERT Solutions Class 12 has covered various kinds of concepts in the chapter.

• Application of Integrals – there are several methods of calculation of functions, differentiation, and integration. Integral has applications in various fields of mathematics, science, engineering, etc. The main and basic application of integration is to calculate areas, area of bounded region, area of curved region, area between two curves. The integral is also theoretically known as the anti-derivative. The integral calculation is the reverse process of the differentiation. There are two types of integrals
  • Definite integral – an integral which contains definite limits,i.e., a specific upper and lower limit is called the definite integral. A definite integral is also known as the Riemann integral.
  • Indefinite integral – such integral whose upper and lower limit is not defined is called the indefinite integral. In the indefinite integral C is the constant term.
• There are many different uses of integral in maths and physics such as it can be used to
  • Calculate the center of mass of an area that is bounded by a curved side.
  • To find the area between two curves.
  • The average value of the curve.
  • Centre of gravity
  •  Mass and momentum and the inertia of any traversing vehicle
  • Mass and momentum of satellite in the orbit
  • Mass and momentum of a tower
  • Centre of mass
  • To calculate thrust
• Area between Two Curves – It is the calculating area bounded by two curve lines. The basic formula to calculate the curve is
  • P: y = f(x)
  • Q: y = g(x)

NCERT Solutions Class 12 Maths has a complete discussion of maths and its related concepts.

Answer 1

NCERT Solutions Class 12 Maths Chapter 8 Applications of Integrals

1. Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and the x-axis.

Answer:

The area of the region bounded by the curve, y² = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD.

2. Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the x-axis in the first quadrant.

Answer:

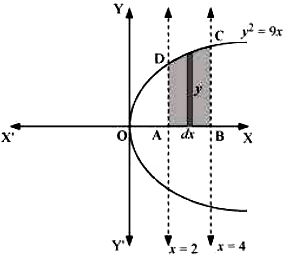
The area of the region bounded by the curve, y² = 9x, x = 2, and x = 4, and the x-axis is the area ABCD.

3. Find the area of the region bounded by x² = 4y, y = 2, y = 4 and the y-axis in the first quadrant.

Answer:

The area of the region bounded by the curve, x² = 4y, y = 2, and y = 4, and the y-axis is the area ABCD.

4. Find the area of the region bounded by the ellipse \(\frac{x^2}{16} + \frac{y^2}{9} = 1\) 

Answer:

The given equation of the ellipse, \(\frac{x^2}{16} + \frac{y^2}{9} = 1\), can be represented as

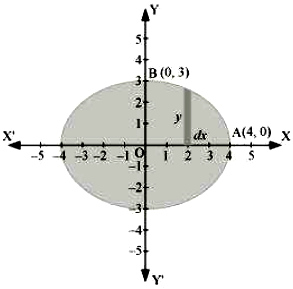
It can be observed that the ellipse is symmetrical about x-axis and y-axis. 

∴ Area bounded by ellipse = 4 × Area of OAB

Therefore, area bounded by the ellipse = 4 × 3π = 12π units

5. Find the area of the region bounded by the ellipse \(\frac{x^2}{4} + \frac{y^2}{9} = 1\)

Answer:

The given equation of the ellipse can be represented as

It can be observed that the ellipse is symmetrical about x-axis and y-axis. 

∴ Area bounded by ellipse = 4 × Area OAB

Therefore, area bounded by the ellipse = \(4 \times \frac{3\pi}2\) = 6π units .

6. Find the area of the region in the first quadrant enclosed by x-axis, line x = √3y and the circle x² + y² = 4.

Answer:

The area of the region bounded by the circle, x² + y² = 4, x = √3y, and the x-axis is the area OAB.

The point of intersection of the line and the circle in the first quadrant is (√3, 1). 

Area OAB = Area ∆OCA + Area ACB

Therefore, area enclosed by x-axis, the line x = √3y, and the circle  x² + y² = 4 in the first quadrant = \(\frac{\sqrt3}2 + \frac\pi3 - \frac{\sqrt3}{2} = \frac\pi3\) units.

7. Find the area of the smaller part of the circle x² + y² = a² cut off by the line \(x = \frac a {\sqrt2}\).

Answer:

The area of the smaller part of the circle, x² + y² = a², cut off by the line, \(x = \frac a {\sqrt2}\), is the area ABCDA.

It can be observed that the area ABCD is symmetrical about x-axis. 

∴ Area ABCD = 2 × Area ABC

Therefore, the area of smaller part of the circle, x² + y² = a², cut off by the line, \(x = \frac a {\sqrt2}\), is \(\frac{a^2}2 \left(\frac\pi2 - 1\right)\) units.

8. The area between x = y² and x = 4 is divided into two equal parts by the line x = a, find the value of a.

Answer:

The line, x = a, divides the area bounded by the parabola and x = 4 into two equal parts.

∴ Area OAD = Area ABCD

It can be observed that the given area is symmetrical about x-axis. 

⇒ Area OED = Area EFCD

From (1) and (2), we obtain

Therefore, the value of a is \((4)^\frac23\).

9. Find the area of the region bounded by the parabola y = x² and y = |x|

Answer:

The area bounded by the parabola, x² = y, and the line, y = |x|, can be represented as

The given area is symmetrical about y-axis. 

∴ Area OACO = Area ODBO 

The point of intersection of parabola, x² = y, and line, y = x, is A (1, 1). 

Area of OACO = Area ∆OAB – Area OBACO

⇒ Area of OACO = Area of ∆OAB – Area of OBACO

\(= \frac12 - \frac13\)

\(= \frac16\)

Therefore, required area = \(2\left[\frac16\right] = \frac13\) units.

10. Find the area bounded by the curve x² = 4y and the line x = 4y – 2.

Answer:

The area bounded by the curve, x² = 4y, and line, x = 4y – 2, is represented by the shaded area OBAO.

Let A and B be the points of intersection of the line and parabola. 

Coordinates of point A are \(\left(-1, \frac14\right)\).

Coordinates of point B are (2, 1). 

We draw AL and BM perpendicular to x-axis. 

It can be observed that, 

Area OBAO = Area OBCO + Area OACO  …(1) 

Then, Area OBCO = Area OMBC – Area OMBO

Similarly, Area OACO = Area OLAC – Area OLAO

Therefore, required area = \(\left(\frac56 + \frac7{24}\right) = \frac98\) units.

Answer 2

11. Find the area of the region bounded by the curve y² = 4x and the line x = 3

Answer:

The region bounded by the parabola, y² = 4x, and the line, x = 3, is the area OACO.

The area OACO is symmetrical about x-axis. 

∴ Area of OACO = 2 (Area of OAB)

Therefore, the required area is 8√3 units.

12. Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is

A. \(\pi\)

B. \(\frac\pi2\)

C. \(\frac\pi3\)

D. \(\frac\pi4\) 

Answer:

Correct option is A. \(\pi\)

The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as

13. Area of the region bounded by the curve y² = 4x, y-axis and the line y = 3 is 

A. 2 

B. \(\frac94\)

C. \(\frac93\)

D. \(\frac92\)

Answer:

Correct option is B. \(\frac94\)

The area bounded by the curve, y² = 4x, y-axis, and y = 3 is represented as

14. Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.

Answer:

The required area is represented by the shaded area OBCDO.

Solving the given equation of circle, 4x² + 4y² = 9, and parabola, x² = 4y, we obtain the point of intersection as \(B\left(\sqrt2, \frac12\right) \) and \(D\left(-\sqrt2, \frac12\right)\).

It can be observed that the required area is symmetrical about y-axis. 

∴ Area OBCDO = 2 × Area OBCO

We draw BM perpendicular to OA. Therefore, the coordinates of M are (√2, 0). 

Therefore, Area OBCO = Area OMBCO – Area OMBO

Therefore, the required area OBCDO is

15. Find the area of the region bounded by the curves y = x² + 2, y = x, x = 0 and x = 3.

Answer:

The area bounded by the curves, y = x² + 2, y = x, x = 0, and x = 3, is represented by the shaded area OCBAO as

Then, Area OCBAO = Area ODBAO – Area ODCO

16. Using integration finds the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).

Answer:

BL and CM are drawn perpendicular to x-axis. 

It can be observed in the following figure that, 

Area (∆ACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)

Equation of line segment AB is

Equation of line segment BC is

Equation of line segment AC is

Therefore, from equation (1), we obtain

Area (∆ABC) = (3 + 5 – 4) = 4 units.

17. Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.

Answer:

The equations of sides of the triangle are y = 2x +1, y = 3x + 1, and x = 4. 

On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13), and C (4, 9).

It can be observed that, 

Area (∆ACB) = Area (OLBAO) –Area (OLCAO)

18. Smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2 is 

A. 2 (π – 2)

B. π – 2 

C. 2π – 1 

D. 2 (π + 2)

Answer:

Correct option is B. π – 2

The smaller area enclosed by the circle, x² + y² = 4, and the line, x + y = 2, is represented by the shaded area ACBA as

It can be observed that, 

Area ACBA = Area OACBO – Area (∆OAB)

19. Area lying between the curve y² = 4x and y = 2x is

A. \(\frac23\)

B. \(\frac13\)

C. \(\frac14\)

D. \(\frac34\) 

Answer:

Correct option is B. \(\frac13\)

The area lying between the curve, y² = 4x and y = 2x, is represented by the shaded area OBAO as

The points of intersection of these curves are O (0, 0) and A (1, 2). 

We draw AC perpendicular to x-axis such that the coordinates of C are (1, 0). 

∴ Area OBAO = Area (∆OCA) – Area (OCABO)

20. Find the area between the curves y = x and y = x².

Answer:

The required area is represented by the shaded area OBAO as

The points of intersection of the curves, y = x and y = x² , is A (1, 1). 

We draw AC perpendicular to x-axis. 

∴ Area (OBAO) = Area (∆OCA) – Area (OCABO)  …(1)

Answer 3

21. Find the area of the region lying in the first quadrant and bounded by y = 4x² , x = 0, y = 1 and y = 4

Answer:

The area in the first quadrant bounded by y = 4x², x = 0, y = 1, and y = 4 is represented by the shaded area ABCDA as

22. Find the area bounded by the curve y = sin x between x = 0 and x = 2π

Answer:

The graph of y = sin x can be drawn as

∴ Required area = Area OABO + Area BCDB

23. Find the area enclosed between the parabola y² = 4ax and the line y = mx

Answer:

The area enclosed between the parabola, y² = 4ax, and the line, y = mx, is represented by the shaded area OABO as

The points of intersection of both the curves are (0, 0) and \(\left(\frac{4a}{m^2}, \frac{4a}m\right)\). 

We draw AC perpendicular to x-axis. 

∴ Area OABO = Area OCABO – Area (∆OCA)

24. Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x + 12.

Answer:

The area enclosed between the parabola, 4y = 3x² , and the line, 2y = 3x + 12, is represented by the shaded area OBAO as

The points of intersection of the given curves are A (–2, 3) and (4, 12). We draw AC and BD perpendicular to x-axis. 

∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)

25. Find the area of the smaller region bounded by the ellipse \(\frac{x^2}{9} + \frac{y^2}4 = 1\) and the line \(\frac x3 + \frac y2 = 1\)

Answer:

The area of the smaller region bounded by the ellipse, \(\frac{x^2}{9} + \frac{y^2}4 = 1\), and the line, \(\frac x3 + \frac y2 = 1\), is represented by the shaded region BCAB as

∴ Area BCAB = Area (OBCAO) – Area (OBAO)

26. Find the area of the smaller region bounded by the ellipse \(\frac {x^2}{a^2}+ \frac{y^2}{b^2} = 1\) and the line \(\frac xa +\frac yb = 1\).

Answer:

The area of the smaller region bounded by the ellipse, \(\frac {x^2}{a^2}+ \frac{y^2}{b^2} = 1\), and the line, \(\frac xa +\frac yb = 1\), is represented by the shaded region BCAB as

∴ Area BCAB = Area (OBCAO) – Area (OBAO)

27. Find the area of the region enclosed by the parabola x² = y, the line y = x + 2 and x-axis.

Answer:

The area of the region enclosed by the parabola, x² = y, the line, y = x + 2, and x-axis is represented by the shaded region OABCO as

The point of intersection of the parabola, x² = y, and the line, y = x + 2, is A (–1, 1). 

∴ Area OABCO = Area (BCA) + Area COAC

28. Using the method of integration find the area bounded by the curve |x| + |y| = 1 

[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]

Answer:

The area bounded by the curve, |x| + |y| = 1, is represented by the shaded region ADCB as

The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0). 

It can be observed that the given curve is symmetrical about x-axis and y-axis. 

∴ Area ADCB = 4 × Area OBAO

29. Using the method of integration find the area of the region bounded by lines: 

2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0

Answer:

The given equations of lines are 2x + y = 4  …(1) 

3x – 2y = 6  …(2) 

And, x – 3y + 5 = 0 …(3)

The area of the region bounded by the lines is the area of ∆ABC. AL and CM are the perpendiculars on x-axis. 

Area (∆ABC) = Area (ALMCA) – Area (ALB) – Area (CMB)

30.  The area bounded by the curve y = x|x|, x-axis and the ordinates x = –1 and x = 1 is given by 

[Hint: y = x² if x > 0 and y = –x² if x < 0]

A. 0 

B. \(\frac13\)

C. \(\frac23\)

D. \(\frac43\)

Answer:

Correct option is C. \(\frac23\)