Correct option is (1) neither one-one nor onto.
\(f(x) = \begin{cases} 1-x,& x<1\\x-1,& x\ge 1\end{cases}\)
\(g(x) = \begin{cases}e^x,& x\ge 0\\x+1,& x\le 0\end{cases}\)
\(f(g(x)) =\begin{cases}1-(x+1), & x< 0\\e^x -1,&x\ge 0 \end{cases}\)
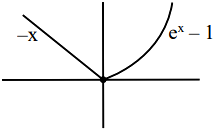
neither one-one nor onto.