Question

A ray of light coming from the point P (1, 2) gets reflected from the point Q on the x-axis and then passes through the point R (4, 3). If the point S (h, k) is such that PQRS is a parallelogram, then \(\text{hk}^2\) is equal to : 

(1) 80 

(2) 90 

(3) 60 

(4) 70

Answer 1

Correct option is : (4) 70 

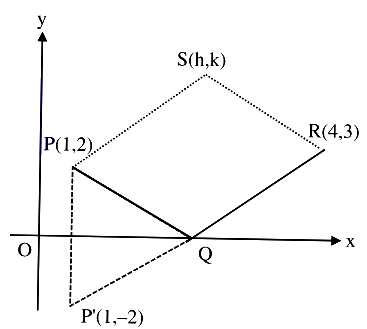
Image of P wrt x-axis will be \( \mathrm{P}^{\prime}(1,-2)\) equation of line joining P'R will be

\(y-3=\frac{5}{3}(x-4)\)

Above line will meet \( \mathrm{x}\)-axis at \(\mathrm{Q}\) where

\(\mathrm{y}=0 \Rightarrow \mathrm{x}=\frac{11}{5}\)

\(\therefore \mathrm{Q}\left(\frac{11}{5}, 0\right)\)

\(\because \mathrm{PQRS}\) is parallelogram so their diagonals will bisects each other 

\(\Rightarrow \frac{4+1}{2}=\frac{\frac{11}{5}+\mathrm{h}}{2} \& \frac{2+3}{2}\) \(=\frac{k+0}{2}\)

\(\Rightarrow \mathrm{h}=\frac{14}{5} \ \&\ \mathrm{k}=5\) 

\( \therefore \mathrm{hk}^{2}=\frac{14}{5} \times 5^{2}=70\)